Epipolar Geometry (에피폴라 기하학)

Epipolar Geometry (에피폴라 기하학)

• Stereo Vision 에서 사용 되는 개념.

• 2개의 pin-hole camera 는 영상 정보에서 depth 정보를 잃어버리게 되는데, 이 때 depth 정보를 얻기 위해 사용.

• 2개의 카메라가 동일한 객체를 바라본다고 가정했을 때, depth 정보를 생성하기 위한 계산을 수행.

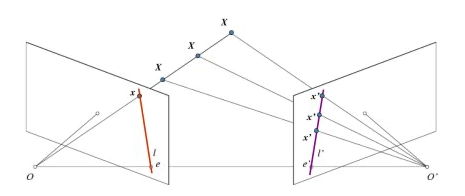
위의 사진을 봤을 때 $X$ 를 바라보는 카메라들이 있다

왼쪽 카메라를 기준으로 $X$ 를 바라볼 때 선분 $OX$ 상에 위치한 모든 점들은 평면상으로 같은 지점에 projection 되게 되므로 depth 정보가 사라진다

이 때 반대편의 카메라에서 $O’$ 에서 $OX$ 상의 점들을 바라보게 되면 평면상으로 다른 지점에 위치하게 되는데, 이 점들에 대해 삼각측량법을 이용하게 되면 ($O$, $O’$, $X$) 삼각형 구도의 꼭대기 부분에 있는 점들에 대해 depth 정보를 취득할 수 있게 된다.

Epipole, Epipolar line, Epipolar plane

• Epipole; 카메라의 중심인 $O$, $O’$ 에서 각 원점에서부터 보여지는 점이 다른 카메라에서 어디에 존재하는지. (두 원점을 잇는 선과 이미지 평면이 만나는 지점 (사진상 $e$, $e’$))
• Epipolar line; 각 카메라에서 Epipole 들을 이은 선분 ($l$, $l’$)
• Epipolar plane; 두 카메라의 원점과 두 카메라 동시에 바라보는 피사체를 이은 평면 ($X$, $O$, $O’$)

Essential Matrix, Fundamental Matrix

• Epipolar 를 찾기 위해선 2개의 매트릭스가 필요.
• Essential Matrix ($E$); 두 카메라에 대한 위치 정보. Translation 과 Rotation.
• Fundametal Matrix ($F$)
  • $E$ 와 동일한 정보를 갖고 있지만 픽셀 좌표로 관계를 나타낼 수 있는 정보 추가.
  • 한 카메라에서 찍은 이미지에서 하나의 점을 다른 이미지의 Epipolar line (Epiline) 으로 대응시켜놓은 매트릭스.
  • 두 개의 이미지를 매칭 시켜 계산할 수 있다.

Code

import cv2
import numpy as np

class Epipolar:
    def __init__(self, img1, img2):
        self.__img1 = img1
        self.__img2 = img2

        self.__feature_detector = cv2.xfeature2d.SIFT_create()
        self.__feature_matcher = cv2.FlannBasedMatcher(dict(algorithm=0, trees=5), dict(checks=50))

    def main(self):
        kp1, des1 = self.__feature_detector.detectAndCompute(self.__img1, None)
        kp2, des2 = self.__Feature_detector.detectAndCompute(self.__img2, None)

        matches = self.__feature_matcher.knnMatch(des1, des2, k=2)

        pts1 = [kp1[m.queryIdx].pt for m, n in matches if m.distance < 0.5 * n.distance]
        pts2 = [kp2[m.trainIdx].pt for m, n in matches if m.distance < 0.5 * n.distance]

        pts1 = np.float32(pts1)
        pts2 = np.float32(pts2)
        
        F, mask = cv2.findFundamentalMat(pts1, pts2, cv2.FM_LMEDS)

        pts1 = pts1[mask.ravel() == 1]
        prs2 = pts2[mask.ravel() == 1]

        lines1 = cv2.computeCorrespondEpilines(pts2.reshape(-1, 1, 2), 2, F)
        lines1 = lines1.reshape(-1, 3)

        lines2 = cv2.computeCorrespondEpilines(pts1.reshape(-1, 1, 2), 1, F)
        lines2 = lines2.reshape(-1, 3)
        
        return pts1, line1, pts2, lines2


if __name__ == '__main__':
    img1 = cv2.imread('path/to/img1.png')
    img2 = cv2.imread('path/to/img2.png')

    epipolar = Epipolar(img1, img2)
    pts1, lines1, pts2, lines2 = epipolar.main()

• 코드에 대한 설명은 빠른 시일내에 작성하도록 하겠다.